Calcul numérique

Rubrique : mathématiques appliquées, algorithme, chaos.

Alternative à cette page, avec des formules accessibles au format XHTML 1.1 + MathML 2.0.
[page expérimentale]

Intégration numérique

But de l’intégration numérique

Le but de l’intégration numérique est de calculer une valeur approchée S_n(f) de l’intégrale I(f) de la fonction f sur un intervalle [a,b] donné, pour une précision donnée.

   

Méthode de GAUSS

Pour un n donné, prenons, pour la fonction f, un polynôme Q∈R_p[X] à valeurs réelles et de degré p et cherchons ∀i∈[1..n] les couples (W_i,x_i) tels que S_n(Q)=I(Q). Pour cela, il faut que le polynôme Q soit de degré p=2n−1.

Sur l’intervalle Ω=[−1,1] et pour tout i∈[1..n], les points x_i — qui sont égaux aux zéros du polynôme de Legendre P_n de degré n sur [−1,1] — et les poids W_i sont donnés par les formules suivantes :

Application à l’intervalle [a,b]

Soit f la fonction à intégrer sur l’intervalle [a,b] :

Nous choisissons un n fixé. Puis, nous allons découper l’intervalle [a,b] en N sous-intervalles de longueur constante d=(b−a)/N. Le scalaire S_N(f), dont l’expression est donnée ci-dessous, est alors une valeur approchée de l’intégrale I(f) sur l’intervalle [a,b].

Un majorant de l’erreur est donné par la formule :

où  

Valeurs numériques de (W_i,x_i)

Valeurs de (W_i,x_i) pour n∈{1,2,3,4,5}

n	Wk	xk
n=1	W1=2	x1=0
n=2	W1=1 W2=1	x1=−1/√3 x2=1/√3
n=3	W1=5/9 W2=8/9 W3=5/9	x1=−√(3/5) x2=0 x3=√(3/5)
n=4	W1= W2= W3= 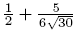W4=	x1= x2= x3= x4=
n=5	W1= W2= W3= W4= W5=	x1= x2= x3=0 x4= x5=

Programmation en C

// DATA
double  W1,W2,W3,x1,x2,x3;
double  S1,S2,S3,X1,X2,X3,S,a,b,d;
double  f(double x);
longint k,N;

// INITIALISATION  for n=3
W1=5/9;  x1=-sqrt(3/5);
W2=8/9;  x2=0;
W3=5/9;  x3=sqrt(3/5);
d = (b-a)/N;
S1 = 0;  X1 = a+0.5*d*(1+x1);
S2 = 0;  X2 = a+0.5*d*(1+x2);
S3 = 0;  X3 = a+0.5*d*(1+x3);

// MAIN LOOP
for(k=0;k<N;k++)
{
    S1 += f(X1);  X1 += d;
    S2 += f(X2);  X2 += d;
    S3 += f(X3);  X3 += d;
}

// RESULT
S = 0.5*d*(W1*S1+W2*S2+W3*S3);

Fiche à télécharger

• Mémento « Intégration numérique – Méthode de Gauss » (PDF, 148 Kio)

Dérivation numérique

Utilisation du développement en séries de Taylor.

But et notations

Le but est de calculer, numériquement, la dérivée d’ordre n de la fonction f au point x₀. De plus, nous pouvons calculer ces formules telle sorte que l’erreur soit en 1/h^p, où p est l’ordre de l’approximation : ce nombre est pair.

Pour (A₀,A₁,…,A_k)∈ N^k+1 et pour un h>0 fixé, voici les formules de dérivation numérique.

Pour n impair

où  

Pour n pair

où  

Exemples

Dérivée première (n=1)

Paramètres pour calculer une dérivée première

p	A0	A1	A2	A3	A4	A5
2	2	1	·	·	·	·
4	12	8	−1	·	·	·
6	60	45	−9	1	·	·
8	840	672	−168	32	−3	·
10	2520	2100	−600	150	−25	2

Dérivée seconde (n=2)

Paramètres pour calculer une dérivée seconde

p	A0	A1	A2	A3	A4	A5
2	1	1	·	·	·	·
4	12	8	−1	·	·	·
6	180	270	−27	2	·	·
8	5040	8064	−1008	128	−9	·
10	25200	42000	−6000	1000	−125	8

Application

Pour utiliser la formule, il faut choisir un h fixe, le plus petit possible de telle sorte que la précision soit la plus grande possible, mais il faut, également, que cette valeur ne soit pas trop petite car elle génèrerai des erreurs d’arrondis qui donneront une valeur de la dérivée complètemenet faussée. Donc, la détermination de la valeur de h se fait de manière empirique à l’aide d’essais.

Fiche à télécharger

• Mémento « Dérivation numérique – Développement en séries de Taylor » (PDF, 123 Kio)

Résolution d’équations différentielles

Équation différentielle d’ordre 1

Voici comment résoudre numériquement l’équation différentielle d’ordre 1 suivante (E) : x′=f(t,x)

Méthode de RUNGE-KUTTA d’ordre 1 ou méthode d’EULER

Méthode de RUNGE-KUTTA d’ordre 2

Méthode de RUNGE-KUTTA d’ordre 3

Méthode de RUNGE-KUTTA d’ordre 4

Système de deux équations différentielles d’ordre 1

Voici comment résoudre numériquement le système (S) de deux équations différentielles d’ordre 1 à deux fonctions inconnues à l’aide de la méthode de RUNGE-KUTTA d’ordre 4.

Équation différentielle d’ordre 2

Voici comment résoudre numériquement l’équation différentielle d’ordre 2 suivante (E) : x″=f(t,x,x′)

Posons     d’où le système 

Fiche à télécharger

• Mémento « Équations différentielles – Méthode de Runge-Kutta » (PDF, 113 Kio)